September 11th, 2017
The Conmebol Qualifiers are reaching the final stretch and fans everywhere cannot stop checking the standings. There are 10 teams and two games left for each one. How many results can arise? They seem not to be a lot, will they? Each team can win, draw or lose. Three states! What is better, come in pairs, if one team wins the other is meant to lose, if one ties the other is meant to tie. Sounds interesting: The state of one team automatically conditions the state of the other. No! This is not quantum entanglement. Don’t be confused, we are in the classical world, we will leave quantum mechanics aside. Here, we will only give basic notions of the theory of probability.
In one matchday there are five games and the results of each one can be 3 (win, draw or lose), how many combinations will be there? The answer is 3 x 3 x 3 x 3 x 3 = 243. This means that in matchday 17 there are 243 ways in which the standings can be left. Wow! That’s not all, in matchday 18 will be the same. So how many combinations are there in total? The answer is 243 x 243 = 59049. Yes, I know, the number is gigantic and we have not considered the number of goals.
The objective is to reduce this number, study all the options available, and determine the teams that will qualify (in this article, a “qualified team” includes the team that advances to the inter-confederation play-offs). Let’s check the games,
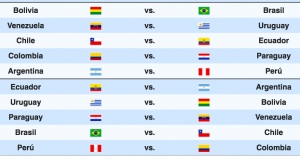
Pay attention to the match Bolivia vs Brazil. Do you think this match will change the standings?
Of course not! Brazil is 1st and Bolivia 9th. We can say that the standings won’t change even if Bolivia wins. Consequently, matchday 17 has only 4 important games. Following the calculations made previously,
- Possible combinations in matchday 17: 3 x 3 x 3 x 3 = 81
- Possible combinations in matchday 18: 3 x 3 x 3 x 3 x 3 = 243
- Total possible combinations: 81 x 243 = 19683
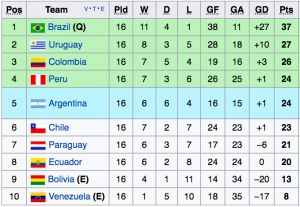
Wow! Instead of 59049 cases we have 19683. We are on the right track. What else can we do? Let’s check the matches of Uruguay. She plays against Venezuela in Caracas and against Bolivia in Montevideo. In addition, her goal difference is much higher than any other team (excluding Brazil). Uruguay needs to win one game to be in the World Cup, and needs to tie one to qualify. It is possible, very easy indeed. Therefore, we are going to assume, without fearing of making any mistake, that Uruguay is already qualified and that Bolivia and Venezuela won’t change the standings even if they win. Therefore, in matchday 17 there are only 3 important games and in matchday 18 only 4. We have,
- Possible combinations in matchday 17: 3 x 3 x 3 = 27
- Possible combinations in matchday 18: 3 x 3 x 3 x 3 = 81
- Total possible combinations: 27 x 81 = 2187
Wow! Instead of 19683 cases we have 2187. Among the remaining games there is one that marks a before and after in the outcome of the Qualifiers. It is the game of Colombia vs Paraguay. If Paraguay wins we would have to analyze 2187 cases because Colombia, being third, could be eliminated. For obvious reasons, this case will be excluded from the analysis. Later we will study the case in which they tie. For now we will consider that Colombia wins in Barranquilla, then Paraguay is eliminated and Colombia qualifies (we will check this premise later). How many cases remain to be analyzed? With Colombia winning, Paraguay’s game against Venezuela becomes irrelevant, so we only have two crucial games in matchday 17 and three in matchday 18. This gives us,
- Possible combinations in matchday 17: 3 x 3 = 9
- Possible combinations in matchday 18: 3 x 3 x 3 = 27
- Total possible combinations: 9 x 27 = 243
That’s right! If Colombia wins we have 243 combinations left. Using all of them we will determine the remaining two teams to qualify. Candidates are, Ecuador, Chile, Argentina, and Peru. The missing games are as follow,
![]() Chile vs Ecuador
Chile vs Ecuador![]()
![]() Argentina vs Peru
Argentina vs Peru![]()
![]() Ecuador vs Argentina
Ecuador vs Argentina![]()
![]() Peru vs ———
Peru vs ———
——— vs Chile![]()
You can see that it doesn’t matter against which teams play Peru and Chile in matchday 18 because their rivals won’t alter the standings. We will now use the theory of probability to know which teams are favorites “mathematically.” Here we are not taking into account historic events, or the fact that one team is in a better position in the FIFA ranking, or the advantage of playing at home. No! Here the result is purely mathematical and the conclusions may go beyond what intuition or belief can dictaminate. Precisely, that’s how the theory of probability was born. Initially, it was believed that chance was determined by a superior being, that if you threw the dice and a six came out, it was meant to be. Over the years, mathematics overcame beliefs, men such as Cardano, Galileo, Pascal, and Fermat laid the first foundations of the theory of probability, which simply indicates that the chances of an event to happen out of a total of N possible probable cases are equal to the ratio between the number of occurrences n of this event (favorable cases) and the total number of possible cases, that is, n / N. Let’s look at some simple examples with the Conmebol Qualifiers.
What is the probability that a team wins its match?
P = 1/3 = 33.3%.
What is the probability that Argentina wins against Peru and Chile wins against Ecuador in matchday 17?
P (![]() ) ∩ P (
) ∩ P (![]() ) = 1/3 x 1/3 = 1/9 = 11.1%.
) = 1/3 x 1/3 = 1/9 = 11.1%.
Since each team can only win (W), draw (D) or lose (L), then the probability of winning is 1 out of 3. And since Argentina and Chile have independent games in matchday 17, the total probability is given by the product, 1 out of 9. This number also indicates that there are nine ways in which Argentina vs Peru and Chile vs Ecuador can be grouped, which are,
A) Chile vs Ecuador (WL) – Argentina vs Peru (WL)
B) Chile vs Ecuador (DD) – Argentina vs Peru (WL)
C) Chile vs Ecuador (LW) – Argentina vs Peru (WL)
D) Chile vs Ecuador (WL) – Argentina vs Peru (DD)
E) Chile vs Ecuador (DD) – Argentina vs Peru (DD)
F) Chile vs Ecuador (LW) – Argentina vs Peru (DD)
G) Chile vs Ecuador (WL) – Argentina vs Peru (LW)
H) Chile vs Ecuador (DD) – Argentina vs Peru (LW)
I) Chile vs Ecuador (LW) – Argentina vs Peru (LW)
Each sub-group is labeled with letters from A to I. WL indicates that the local team wins, DD indicates a tie, and LW indicates that the visitor team wins.
What is the probability of obtaining H?
P (H) = 1/9 = 11.1%
On matchday 18 what could happen? There are 27 possible consequences for each sub-group. The results are detailed in the supplementary file. Click here to see the 243 possible combinations.
What is the probability of obtaining A and then Peru beats Colombia?
P (A) ∩ P (![]() ) = 1/9 x 9/27 = 9/243 = 3.7%
) = 1/9 x 9/27 = 9/243 = 3.7%
Having studied the data shown in the supplementary file, the most interesting conclusions from the theory of probability are,
I. Results strongly depend on goal difference
We just need to look at Tables A.2, B.2, C.2, D.2, E.2, F.2, G.2, H.2, and I.2 in the supplementary information. One can appreciate that the qualifying probability increases considerably by having a better goal difference. This is expected since Argentina, Chile, and Peru have almost the same amount of points, and what is worse, they have the same goal difference. Therefore, teams that manage to score two goals or more in their matches may considerably increase their options to reach the World Cup.
II. Peru is almost qualified if she wins her match against Argentina
Let’s see the results of sub-group G where Peru beats Argentina and Chile beats Ecuador,
| Qualifying probability | If Brazil beats Chile | If Brazil ties Chile | If Chile beats Brazil |
| 3/9 | 0 (3/9) | 0 (1/9) | |
| 9/9 | 8/9 (9/9) | 8/9 (9/9) | |
| 0 | 0 | 0 | |
| 6/9 | 6/9 (9/9) | 9/9 |
As shown in Table G.2, the qualifying probability of Peru ranges from 89% to 100%, and this is considering that she may lose against Colombia. The values in parentheses show the probability in case the team has the best goal difference. Therefore, Peru qualifies, even if Chile beats Brazil, as long as she beats Argentina with a goal difference of 2 (assuming that the others win by 1).
What happens if Peru ties Argentina? The results of sub-group D, where Peru ties Argentina and Chile beats Ecuador, show:
| Qualifying probability | If Brazil beats Chile | If Brazil ties Chile | If Chile beats Brazil |
| 4/9 (7/9) | 4/9 (6/9) | 3/9 (6/9) | |
| 4/9 (7/9) | 4/9 (6/9) | 3/9 (6/9) | |
| 0 | 0 | 0 | |
| 3/9 (8/9) | 8/9 | 9/9 |
The qualifying probability ranges from 3/9 to 4/9. However, Peru’s chances increase up to 7/9 if she has the best goal difference, meaning, if she beats Colombia with a goal difference of 2 or more. Therefore, to avoid complex scenarios, Peru must beat Argentina and consequently forget about Colombia.
III. Argentina needs to beat Peru to be (almost) qualified
Like Peru, Argentina’s odds range from 89% to 100%. Consider the results of sub-group A where Argentina beats Peru and Chile beats Ecuador,
| Qualifying probability | If Brazil beats Chile | If Brazil ties Chile | If Chile beats Brazil |
| 9/9 | 8/9 (9/9) | 8/9 (9/9) | |
| 3/9 | 3/9 (6/9) | 0 | |
| 0 | 0 | 0 | |
| 6/9 | 6/9 (9/9) | 9/9 |
As seen from the Table, even if Chile beats Brazil, the qualifying probability of Argentina oscillates between 8/9 and 9/9. Therefore, we can conclude that the match Argentina vs Peru is an important game where the winner, no matter what happens in the other games, regardless that she loses her last game, is practically qualified. And the loser (as seen from Tables A.2 and G.2), reaching as much 3/9, is left with Chile for the last qualifying spot (in case Chile beats Ecuador).
IV. Chile depends on her goals
As seen from the Tables above (A.2, D.2, and G.2), if Chile thrash Ecuador her qualifying probability increases considerably and it doesn’t matter what happens with the match Argentina vs Peru, because regardless of this, her qualifying probability remains above of one or both teams.
V. Ecuador is on the edge of the abyss
Ecuador can survive beating Chile. By doing so, her qualifying probability can reach values of 3/9 = 33.3%. The curious thing is that if Ecuador ties, there is still a chance for her to qualify, but she must wait for Peru to beat Argentina and on her last match she must thrash her rival (see Table H.1 in the supplementary information). If Ecuador loses in Santiago, her options are over.
Let us now answer the following questions:
- What happens if Colombia ties Paraguay?
The points of the “last qualified team” ranges from 24 to 29 (in the following question we detail these numbers), which shows that Colombia qualifies beating Paraguay. In case of a tie, Colombia would make 27 points (losing against Peru) and Paraguay would reach 25 (beating Venezuela in her last match). Within all the combinations shown in the supplementary file, the upper bound of the “best eliminated team” is 28 points, but only occurs once among all the 243 possibilities. It happens when Argentina and Peru tie in matchday 17 and everybody wins (except Ecuador) on matchday 18. If this is not the case, Colombia would be almost qualified, and I say almost because there are 20 combinations out of 243 in which the “best eliminated team” gets 27 points, the same points as Colombia. Therefore, the qualification will depend on the goal difference and, luckily for the parceros, they arrive well in this aspect as they have a superior number compared to their rivals. Consequently, the chances of Colombia are very high even if she loses against Peru and ties Paraguay.
Paraguay, on the other hand, would reach 25 points as much (tying Colombia and winning against Venezuela), with this number Paraguay could qualify. However, remember that Paraguay has a goal difference of -6; therefore, to qualify she requires to beat Venezuela 7-0. The easiest option is to think about the probability of Paraguay to qualify without thinking of goal differences, this means, we need to check in how many cases the “last qualified team” has 24 points, in order for Paraguay to surpass this team with her points. This leads us to answer the following question first.
2. How many points is likely to have the last qualified team?
For this we will use the tree diagram. There are 9 sub-groups (labeled from A to I). In each sub-group we calculate the probability, P(X), of reaching the last qualifying position with X points (see Tables A.3, B.3, C.3, D.3, E.3, F .3, G.3, H.3, I.3 in the supplementary information). We have:

For example, P(29) indicates the probability of obtaining 29 points in the last qualifying spot (fifth position).
What is the probability of obtaining 29 points through A in the last qualifying position?
P (A ∩ 29) = P (A) x P (29 / A) = 1/9 x 3/27 = 3/243 = 1.2%.
This is known as a conditional probability because we want to find a value by conditioning it to appear from one of the branches of the tree. Its result is given by the probability of obtaining A multiplied by the probability of obtaining 29 points in A. It is usually denoted P (A ∩ 29). Then, the total probability of obtaining 29 across all branches would be the sum of each of them, i.e., P (29) = P (A ∩ 29) + P (B ∩ 29) + P (C ∩ 29) + P (D ∩ 29) + P (E ∩ 29) + P (F ∩ 29) + P (G ∩ 29) + P (H ∩ 29) + P (I ∩ 29). Doing this for all values we get:
P (29) = 6/243
P (28) = 19/243
P (27) = 85/243
P (26) = 75/243
P (25) = 48/243
P (24) = 10/243
Therefore, it is likely that the 5th place in the Conmebol Qualifiers will have 27 points, P (27) = 85/243 = 35%. From here we can culminate the previous analysis. We said that for Paraguay to qualify she needs to reach the qualifying position without paying attention to her goal difference. That is, the chances of Paraguay are reduced to P (24) = 10/243 = 4%. A probability so low that it is better to accept the reality of saying goodbye to the World Cup. Therefore, a tie between Colombia and Paraguay does not greatly affect the results shown in this article. We initially said that Uruguay would be qualified by making just one point in her last two matches. If this happens Uruguay would reach 28 points with a goal difference that is far superior than the others. Consequently, the probability of being eliminated is P (29) = 6/243 = 2.5%. The funny thing is that for this to happen Chile must beat Brazil. Therefore, getting one point in two games should not cause any concern to Uruguay.
3. Which teams will qualify?
Mathematics indicates that Argentina, Chile and Peru are the ones fighting for the last qualifying spots (Ecuador is left behind for having a very low probability). Two out of three wil take their songs to the World Cup. Will Chile sing, “prepárate Rusia que aquí vamos por más“? Or Peru will shout, “porque yo creo en ti, ¡vamos vamos Perú!” Or it will be Argentina who will say, “esta barra quilombera no te deja de alentar.” The total qualifying probability of each team is,
| with the best goal difference | with the worst goal difference |
P(
|
P(
|
The analysis is similar to the tree diagram developed previously, here we only show the results for simplicity (based on the data in Tables A.2, B.2, C.2, D.2, E.2, F.2, G.2, H.2, and I.2 in the supplementary information). The interesting thing is that although Argentina and Peru have the same amount of points before playing their matches, once they finish them, the qualifying probability of Peru is higher. The reason is because Argentina plays against direct rivals whereas Peru, in the last match, does it with a “qualified team.” Another interesting detail is to see how it affects to have the best goal difference. Chile proves to be the most benefited with this, increasing 18.1% its qualifying probability just by scoring more goals, in contrast, Peru and Argentina increase their qualifying probability by 15.3% and 13.6%, respectively; therefore, to use this advantage, the Chileans should focus on thrashing Ecuador at home. By doing so, they will have the best goal difference and therefore they will be 2.8% below Argentina or 3.6% below Peru (since one of them shall have the worst goal difference). Nonetheless, Chile still has the lowest qualifying probability (excluding Ecuador), although we have included the possibility of them beating Brazil in Sao Paulo. If we assume that these results are decisive, we can conclude that the 5 qualified teams will be: Brazil, Uruguay, Colombia, Peru and Argentina. The pending question would be, which team qualifies directly? Peru or Argentina? Carrying out a similar analysis to the previous one we have:
| with the best goal difference | with the worst goal difference |
| P( P( |
P( P( |
Argentina gets a slightly higher probability of occupying the 4th place in the Qualifiers. The reason is the same as the previous case and takes relevance in sub-group F (see supplementary information). If this slight advantage is meant to be a determining factor, Peru would end up facing New Zealand on November 11th. The Inca team led by Gareca would get in the plane and make the most bizarre trip of their lives. They would cross the Pacific with the clock from Santiago telling them that it takes 12 but instead it will last more than one day, and their way back will happen with their watches moving counterclockwise, but that would not matter… because Spain 82′ could finally be left behind.
Christian Ortiz, PhD.
